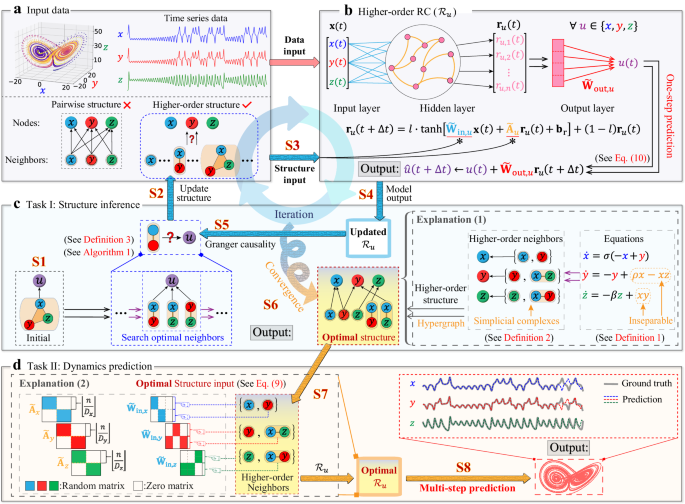
Higher-order Granger reservoir computing: simultaneously achieving scalable complex structures inference and accurate dynamics prediction
Classical reservoir computing We start with a nonlinear dynamical network of N variables of the following general form, $$\dot{{{{{{{{\bf{x}}}}}}}}}(t)={{{{{{{\boldsymbol{f}}}}}}}}[{{{{{{{\bf{x}}}}}}}}(t)],$$ (1) where \({{{{{{{\bf{x}}}}}}}}(t)={[{x}_{1}(t),\ldots,{x}_{N}(t)]}^{\top }\) denotes the N-dimensional (N-D) state of the system at time t, and \({{{{{{{\boldsymbol{f}}}}}}}}[{{{{{{{\bf{x}}}}}}}}(t)]={\left({f}_{1}[{{{{{{{\bf{x}}}}}}}}(t)],{f}_{2}[{{{{{{{\bf{x}}}}}}}}(t)],\ldots,{f}_{N}[{{{{{{{\bf{x}}}}}}}}(t)]\right)}^{\top }\) is the N-D nonlinear vector field. In this article, we assume that neither the vector field f (equivalently, …