Universal scaling between wave speed and size enables nanoscale high-performance reservoir computing based on propagating spin-waves

Physical system of a magnetic device

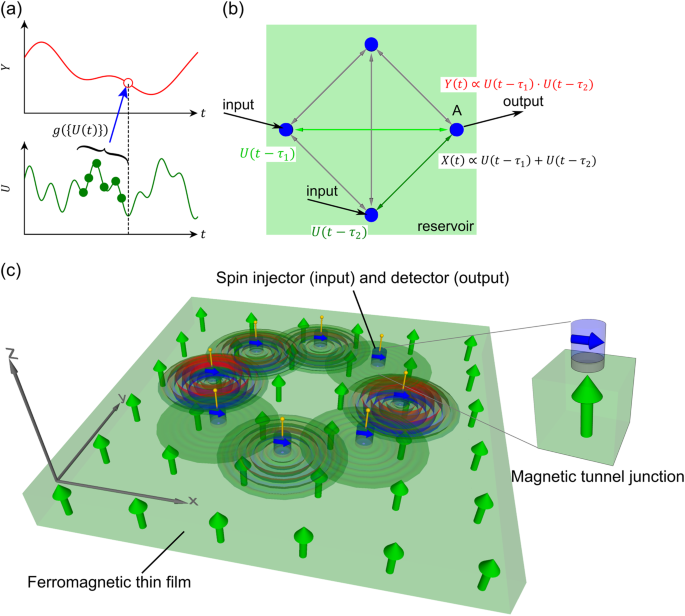
We consider a magnetic device of a thin rectangular system with cylindrical injectors (see Fig. 1c). The size of the device is L × L × D. Under the uniform external magnetic field, the magnetization is along the z direction. Electric current translated from time series data is injected at the N_p injectors with the radius a and the same height D as the device. The spin-torque by the current drives magnetization m(x, t) and propagating spin-waves as schematically shown in Fig. 1c. The magnetization is detected at the same cylindrical nanocontacts as the injectors. The nanocontacts of the inputs and outputs are located on the circle with its radius R (see Fig. 2-(3)). The size of our system is L = 1000 nm and D = 4 nm. We set a = 20 nm unless otherwise stated. We set R = 250 nm in Performance of tasks for MC, IPC, NARMA10, and prediction of chaotic time-series section but R is varied in Scaling of system size and wave speed section as a characteristic length scale.

Details of preprocessing input data

In the time-multiplexing approach, the input time-series \({{{\bf{U}}}}=({U}_{1},{U}_{2},\ldots ,{U}_{T})\in {{\mathbb{R}}}^{T}\) is translated into piece-wise constant time-series \(\tilde{U}(t)={U}_{n}\) with t = (n−1)N_vθ + s under k = 1,…,T and s = [0, N_vθ) (see Fig. 2–(1)). This means that the same input remains during the time period τ₀ = N_vθ. To use the advantage of physical and virtual nodes, the actual input j_i(t) at the ith physical node is U(t) multiplied by τ₀-periodic random binary filter \({{{{\mathcal{B}}}}}_{i}(t)\). Here, \({{{{\mathcal{B}}}}}_{i}(t)\in \{0,1\}\) is piece-wise constant during the time θ. At each physical node, we use different realizations of the binary filter as in Fig. 2-(2). The input masks play a role as the input weights for the ESN without virtual nodes. Because the different masks are used for the different physical nodes, each physical and virtual node may have different information about the input time series.

The masked input is further translated into the input for the physical system. Although numerical micromagnetic simulations are performed in discrete time steps, the physical system has continuous-time t. The injected current density j_i(t) at time t for the ith physical node is set as \({j}_{i}(t)=2{j}_{c}{\tilde{U}}_{i}(t)=2{j}_{c}{{{{\mathcal{B}}}}}_{i}(t)U(t)\) with j_c = 2 × 10⁻⁴/(πa²)A/m². Under a given input time series of the length T, we apply the constant current during the time θ, and then update the current at the next step. The same input current with different masks is injected for different virtual nodes. The total simulation time is, therefore, TθN_v.

Micromagnetic simulations

We analyze the magnetization dynamics of the Landau-Lifshitz-Gilbert (LLG) equation using the micromagnetic simulator mumax^3 61. The LLG equation for the magnetization M(x, t) yields

In the micromagnetic simulations, we analyze Eq. (10) with the effective magnetic field H_eff = H_ext + H_demag + H_exch consists of the external field, demagnetization, and the exchange interaction. The concrete form of each term is

where H_ext is the external magnetic field, H_ms is the magnetostatic interaction, and H_exch is the exchange interaction with the exchange parameter A_ex. The spin waves are driven by Slonczewski spin-transfer torque⁶², which is described by the last term of Eq. (10). The driving term is proportional to the DC current, namely, J(x, t) = j_i(t) at the ith nanocontact and J(x, t) = 0 other regions.

Parameters in the micromagnetics simulations are chosen as follows: The number of mesh points is 200 in the x and y directions, and 1 in the z direction. We consider Co₂MnSi Heusler alloy ferromagnet, which has a low Gilbert damping and high spin polarization with the parameter A_ex = 23.5 pJ/m, M_s = 1000 kA/m, and α = 5 × 10^{−4 51,52,53,63,64}. Out-of-plane magnetic field μ₀H₀ = 1.5 T is applied so that magnetization is pointing out-of-plane. The spin-polarized current field is included by the Slonczewski model⁶² with polarization parameter P = 1 and spin torque asymmetry parameter λ = 1 with the reduced Planck constant ℏ and the charge of an electron e. The uniform fixed layer magnetization is m_f = e_x. We use absorbing boundary layers for spin waves to ensure the magnetization vanishes at the boundary of the system⁶⁵. We set the initial magnetization as m = e_z. The magnetization dynamics is updated by the fourth-order Runge-Kutta method (RK45) under adaptive time-stepping with the maximum error set to be 10⁻⁷.

The reference time scale in this system is t₀ = 1/γμ₀M_s ≈ 5 ps, where γ is the gyromagnetic ratio, μ₀ is permeability, and M_s is saturation magnetization. The reference length scale is the exchange length l₀ ≈ 5 nm. The relevant parameters are Gilbert damping α, the time scale of the input time series θ (see Section Learning with reservoir computing), and the characteristic length between the input nodes R.

Theoretical analysis using response function

To understand the mechanism of high performance of learning by spin wave propagation, we also consider a model using the response function of the spin wave dynamics. By linearizing the magnetization around m = (0, 0, 1) without inputs, we may express the linear response of the magnetization at the ith readout m_i = m_x,i + im_y,i to the input as

where the response function G_ij for the same node is

and for different nodes,

The detailed derivation of the response function is shown in Supplementary Information Section VII. Here, U^(j)(t) is the input time series at jth nanocontact. The response function has a self part G_ii, that is, input and readout nanocontacts are the same, and the propagation part G_ij, where the distance between the input and readout nanocontacts is ∣R_i−R_j∣. In Eqs. (16) and (17), we assume that the spin waves propagate only with the dipole interaction. We discuss the effect of the exchange interaction in Supplementary Information Section VII A. We should note that the analytic form of Eq. (17) is obtained under certain approximations. We discuss its validity in Supplementary Information Section VII A.

We use the quadratic nonlinear readout, which has a structure

The response function of the nonlinear readout is \({G}_{i{j}_{1}{j}_{2}}^{(2)}(t,{t}_{1},{t}_{2})\propto {G}_{i{j}_{1}}(t,{t}_{1}){G}_{i{j}_{2}}(t,{t}_{2})\). The same structure as Eq. (18) appears when we use a second-order perturbation for the input (see Supplementary Information Section V A). In general, we may include the cubic and higher-order terms of the input. This expansion leads to the Volterra series of the output in terms of the input time series, and suggests how the spin wave RC works as shown in Methods: Relation of MC and IPC with learning performance (see also Supplementary Information Section II for more details). Once the magnetization at each nanocontact is computed, we may estimate MC and IPC.

We also use the following Gaussian function as a response function,

where R_ij is the distance between ith and jth physical nodes. The Gaussian function Eq. (19) has its mean t = R_ij/v and variance w². Therefore, w is the width of the Gaussian function (see Fig. 6e). We set the width as w = 50 in the normalized time unit t₀. In Supplementary Information Section VII A, we introduce the skew normal distribution, which generalize Eq. (19) to include the effect of exchange interaction.

Learning tasks

NARMA task

The NARMA10 task is based on the discrete differential equation,

Here, U_n is an input taken from the uniform random distribution \({{{\mathcal{U}}}}(0,0.5)\), and Y_n is an output. We choose the parameter as α = 0.3, β = 0.05, γ = 1.5, and δ = 0.1. In RC, the input is U = (U₁, U₂,…,U_T) and the output Y = (Y₁, Y₂,…, Y_T). The goal of the NARMA10 task is to estimate the output time-series Y from the given input U. The training of RC is done by tuning the weights W so that the estimated output \(\hat{Y}({t}_{n})\) is close to the true output Y_n in terms of squared norm \(| \hat{Y}({t}_{n})-{Y}_{n}{| }^{2}\).

The performance of the NARMA10 task is measured by the deviation of the estimated time series \(\hat{{{{\bf{Y}}}}}={{{\bf{W}}}}\cdot \tilde{\tilde{{{{\bf{X}}}}}}\) from the true output Y. The normalized root-mean-square error (NRMSE) is

Performance of the task is high when NRMSE≈0. In the ESN, it was reported that NRMSE ≈ 0.4 for N = 50 and NRMSE ≈ 0.2 for N = 200³¹. The number of node N = 200 was used for the speech recognition with ≈0.02 word error rate³¹, and time-series prediction of spatio-temporal chaos⁶. Therefore, NRMSE ≈ 0.2 is considered as reasonably high performance in practical application. We also stress that we use the same order of nodes (virtual and physical nodes) N = 128 to achieve NRMSE ≈ 0.2.

Memory capacity (MC)

MC is a measure of the short-term memory of RC. This was introduced in ref. ⁷. For the input U_n of random time series taken from the uniform distribution, the network is trained for the output Y_n = U_n−k. Here, U_n−k is normalized so that Y_n is in the range [–1,1]. The MC is computed from

This quantity is decaying as the delay k increases, and MC is defined as

Here, \({k}_{\max }\) is a maximum delay, and in this study we set it as \({k}_{\max }=100\). The advantage of MC is that when the input is independent and identically distributed (i.i.d.), and the output function is linear, then MC is bounded by N, the number of internal nodes⁷.

We show the example of MC_k as a function of k and IPC_j as a function of k₁ and k₂ in Fig. S2a and b. When the delay k is short, MC_k ≈ 1 suggesting that the delayed input can be reconstructed by the input without the delay. When delay becomes longer reservoir does not have capacity to reconstruct delayed input, however, MC_k and IPC_j defined by Eqs. (22) and (25) have long tail small positive values, making overestimation of MC and IPC. To avoid the overestimation, we use the threshold value ε = 0.03727 below which we set MC_k = 0. The value of ε is set following the argument of ref. ²⁶. When the total number of readouts is N(=128) and the number of time steps to evaluate the capacity is T(=5000), the mean error of the capacity is estimated as N/T. We assume that the distribution of the error yields χ² distribution as (1/T)χ²(N). Then, we may set ε such that \(\varepsilon =\tilde{N}/T\) where \(\tilde{N}\) is taken from the χ² distribution and the probability of its realization is 10⁻⁴, namely, \(P(\tilde{N} \sim {\chi }^{2}(N))=1{0}^{-4}\). In fact, Fig. S2a demonstrates that when the delay is longer, the capacity converges to N/T and fluctuates around the value. In this regime, we set MC_k = 0 and do not count for the calculation of MC. The same argument applies to the calculation of IPC.

Information processing capacity (IPC)

IPC is a nonlinear version of MC²⁶. In this task, the output is set as

where d_k is non-negative integer, and \({{{{\mathcal{P}}}}}_{{d}_{k}}(x)\) is the Legendre polynomials of x order d_k. As MC, the input time series is uniform random noise \({U}_{n}\in {{{\mathcal{U}}}}(0,0.5)\) and then normalized so that Y_n is in the range [–1,1]. We may define

and then compute jth order IPC as We may define

When j = 1, the IPC is, in fact, equivalent to MC, because \({{{{\mathcal{P}}}}}_{0}(x)=1\) and \({{{{\mathcal{P}}}}}_{1}(x)=x\). In this case, Y_n = U_n−k for d_i = 1 when i = k and d_i = 0 otherwise. Equation (26) takes the sum over all possible delay k, which is nothing but MC. When j > 1, IPC_j captures the nonlinear transformation and delays up of the jth polynomial order. For example, when j = 2, the output can be \({Y}_{n}={U}_{n-{k}_{1}}{U}_{n-{k}_{2}}\) or \({Y}_{n}={U}_{n-k}^{2}+{{{\rm{const.}}}}\) In this study, we focus on j = 2 because the second-order nonlinearity is essential for the NARMA10 task (see Supplementary Information Section I). In ref. ²⁶, IPC is defined by sum of IPC_j over j. In this study, we focus only on IPC₂, which plays a relevant role for the NARMA10 task (see Supplementary Information Section I). We denote IPC and IPC₂ interchangeably.

The example of IPC₂ as a function of the two delay times k₁ and k₂ is shown in Fig. S2b. When both k₁ and k₂ are small, the nonlinear transformation of the delayed input \({Y}_{n}={U}_{n-{k}_{1}}{U}_{n-{k}_{2}}\) can be reconstructed from U_n. As the two delays are longer, IPC₂ approaches the value N/T of systematic error. As we performed for the MC task, we define the same threshold ε, and do not count the capacity below the threshold in IPC₂.

Prediction of chaotic time-series data

Following ref. ⁶, we perform the prediction of time-series data from the Lorenz model. The model is a three-variable system of (A₁(t), A₂(t), A₃(t)) yielding the following equation

The parameters are chosen such that the model exhibits chaotic dynamics. Similar to the other tasks, we apply the different masks of binary noise for different physical nodes, \({{{{\mathcal{B}}}}}_{i}^{(l)}(t)\in \{-1,1\}\). Because the input time series is three-dimensional, we use three independent masks for A₁, A₂, and A₃, therefore, l ∈ {1, 2, 3}. The input for the ith physical node after the mask is given as \({{{{\mathcal{B}}}}}_{i}(t){\tilde{U}}_{i}(t)={{{{\mathcal{B}}}}}_{i}^{(1)}(t){A}_{1}(t)+{{{{\mathcal{B}}}}}_{i}^{(2)}(t){A}_{2}(t)+{{{{\mathcal{B}}}}}_{i}^{(3)}(t){A}_{3}(t)\). Then, the input is normalized so that its range becomes [0, 0.5], and applied as an input current. Once the input is prepared, we may compute magnetization dynamics for each physical and virtual node, as in the case of the NARMA10 task. We note that here we use the binary mask of {−1, 1} instead of {0, 1} used for other tasks. We found that the {0,1} does not work for the prediction of the Lorenz model, possibly because of the symmetry of the model.

The ground-truth data of the Lorenz time-series is prepared using the Runge-Kutta method with the time step Δt = 0.025. The time series is t ∈ [−60, 75], and t ∈ [−60, −50] is used for relaxation, \(t\in \left(-50,0\right]\) for training, and \(t\in \left(0,75\right]\) for prediction. During the training steps, we compute the output weight by taking the output as Y = (A₁(t + Δt), A₂(t + Δt), A₃(t + Δt)). After training, the RC learns the mapping (A₁(t), A₂(t), A₃(t)) → (A₁(t + Δt), A₂(t + Δt), A₃(t + Δt)). For the prediction steps, we no longer use the ground-truth input but the estimated data \((\hat{{A}_{1}}(t),\hat{{A}_{2}}(t),\hat{{A}_{3}}(t))\) as schematically shown in Fig. 5c. Using the fixed output weights computed in the training steps, the time evolution of the estimated time-series \((\hat{{A}_{1}}(t),\hat{{A}_{2}}(t),\hat{{A}_{3}}(t))\) is computed by the RC.

Relation of MC and IPC with learning performance

The relevance of MC and IPC is clear by considering the Volterra series of the input-output relation. The input-output relationship is generically expressed by the polynomial series expansion as

Each term in the sum has k_n power of U_n. Instead of polynomial basis, we may use orthonormal basis such as the Legendre polynomials

Each term in Eqs. (30) and (31) is characterized by the non-negative indices (k₁, k₂,…,k_n). Therefore, the terms corresponding to j = ∑_ik_i = 1 in Y_n have information on linear terms with time delay. Similarly, the terms corresponding to j = ∑_ik_i = 2 have information of second-order nonlinearity with time delay. In this view, the estimation of the output Y(t) is nothing but the estimation of the coefficients \({\beta }_{{k}_{1},{k}_{2},\ldots ,{k}_{n}}\).

Here, we show how the coefficients can be computed from the magnetization dynamics. In RC, the readout of the reservoir state at ith node (either physical or virtual node) can also be expanded as the Volterra series

where \({\tilde{\tilde{X}}}^{(i)}({t}_{n})\) is measured magnetization dynamics and U_n is the input that drives spin waves. At the linear and second-order in U_k, Eq. (32) is discrete expression of Eqs. (15) and (18). By comparing Eqs. (30) and (32), we may see that MC and IPC are essentially a reconstruction of \({\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}\) from \({\tilde{\tilde{\beta }}}_{{k}_{1},{k}_{2},\cdots \,,{k}_{n}}^{(i)}\) with i ∈ [1, N]. This can be done by regarding \({\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}\) as a T + T(T−1)/2+⋯-dimensional vector, and using the matrix M associated with the readout weights as

MC corresponds to the reconstruction of \({\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}\) for ∑_i k_i = 1, whereas the second-order IPC is the reconstruction of \({\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}\) for ∑_ik_i = 2. If all of the reservoir states are independent, we may reconstruct N components in \({\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}\). In realistic cases, the reservoir states are not independent, and therefore, we can estimate only <N components in \({\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}\). For more details, readers may consult Supplementary Information Sections I and II.