Resource analysis scheme
As the current level of physical quantum gates has a very high error rate, techniques such as QEC code and MSD should be used to create logical qubits and logical operations with low error rates. We performed a resource analysis using the physical-level analysis method and the equation for the required resources used in article31. In this section, we briefly introduce the techniques used for this physical-level analysis and introduce a closed-form formula for \(N_{phy}\) and \(T_r\).
As mentioned above, we used QEC code to generate a logical qubit with a low gate error rate. We selected a rotated planar surface code from a variety of QEC codes36. The number of physical qubits required to construct one logical qubit is \(2d^2-1\) when the code distance is d. The following relationship is established between the d, \(\epsilon _p\), and logical gate error rate \(\epsilon _L\) required by the algorithm in the rotated surface code8.
$$\begin{aligned} d=2\cdot \lceil \frac{\log (10\epsilon _{L})}{\log (100\epsilon _p)}\rceil -1. \end{aligned}$$
(2)
In Eq. (2), \(\lceil x \rceil\) is the function that takes real number x as an input and returns the least integer greater than or equal to x. Therefore, we can determine the distance of the surface code using KQ formalism to obtain the \(\epsilon _L\) required by the algorithm.
To perform the T gate with a low error rate in QEC codes, the \(|A\rangle = |0\rangle +\exp (i\cdot \pi /4)|1\rangle\) state with a low error rate is required. MSD uses multiple noisy \(|A\rangle\) states and outputs a smaller number of more reliable \(|A\rangle\) states.
As in article31, we used Fowler and Gidneyâs MSD protocol8. We performed various levels of MSD based on the \(\epsilon _L\) required by the algorithm. The code distances for MSD \(d_1\), \(d_2\), and \(d_3\) all have odd values greater than or equal to 15. As shown in Table 2, the number of physical qubits required to make one T gate, \(T_m\), and the time required for MSD, \(t_T\), are expressed as functions of \(d_1\), \(d_2\), and \(d_3\). In Table 2, \(c_t\) denotes the cycle time of the surface code8. Many studies have assumed that \(c_t=200\) ns26,30, and we have adopted that assumption. We set \(d_1\), \(d_2\), and \(d_3\) such that \(T_m\) is as minimal as possible while still satisfying the \(\epsilon _L\) requirement. As the \(T_m\) increased dramatically when the distillation level increased, we adjusted the code distances to perform distillation at the lowest possible level.
As shown in article31, the \(N_{phy}\) and the \(T_r\) can be expressed as
$$\begin{aligned} N_{phy}&=(2\cdot (2\lceil \frac{\log (\frac{10 p_{fail}}{KQ})}{\log (100\epsilon _p)}\rceil -1)^2-1)\cdot (K+N_{CNOT})+N_T\cdot T_m, \end{aligned}$$
(3)
$$\begin{aligned} T_r&=\frac{D\cdot t_T}{1-p_{fail}}. \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \end{aligned}$$
(4)
In Eq. (3), K is the number of logical qubits required by the algorithm, \(N_{CNOT}\) is the maximum number of concurrent CNOT gates, and \(N_T\) is the maximum number of concurrent T gates. In Eq. (4), D is the T depth of the algorithm. In Eqs. (3) and (4), \(p_{fail}\) is the probability of the failure of the algorithm. When elliptic curve logarithms on an elliptic curve is defined over n-bit prime field, the RA has \(K=9n+2\lceil \log _2 (n) \rceil +10\).
Decomposition of algorithm at the logical level
Similar to the analysis used in article31, the algorithm is decomposed into X, Z, CNOT, and T gates, and the \(\epsilon _L\) for the algorithm to operate properly is obtained using KQ formalism. Using this logical gate error rate obtained through KQ formalism, we can determine the distance of the surface code and the level and distance of the MSD. In addition, we obtained the T depth to identify the \(T_r\). To determine the number of magic-state factories to be prepared, we counted \(N_T\). Considering the CNOT operation using the lattice surgery method36, we also determined that the \(N_{CNOT}\).
KQ formalism is described as follows38:
$$\begin{aligned} p_{fail}=KQ\epsilon _L. \end{aligned}$$
(5)
In Eq. (5), \(p_{fail}\) is the algorithm failure probability. We can determine \(\epsilon _{L}\) by obtaining K and Q. Previous studies have performed analyses using \(p_{fail}\) as a fixed value27,28. On the contrary, we set \(p_{fail}\) as a variable to confirm the change in the required resources of the algorithm according to the change in \(p_{fail}\).
Because the values of K and Q depend on the algorithm, we decomposed the RA to obtain K and Q. First, we confirmed that decomposing the Toffoli gate using the method presented in article39 would result in Q of 11 and T depth of 3. The majority of the operations in the RA are modular operations that require a constant adder gate. In 2016, Häner et al. developed a quantum constant adder using a divide-and-conquer method32. Hänerâs constant adder includes serial and parallel versions, and the RA uses a serial version of a constant adder. The elementary gate step \(Q_{Roe}\) and T depth \(D_{Roe}\) of the RA are expressed as follows (Please see supplementary information).
$$\begin{aligned} Q_{Roe}&=2472n^3\log _2 n+10316n^3+1442n^2\log _2 n-2222n^2,\end{aligned}$$
(6)
$$\begin{aligned} D_{Roe}&=576n^3\log _2 n+2796n^3+336n^2\log _2 n-510n^2. \end{aligned}$$
(7)
As the CNOT gates are serially executed in the Takahashi adder, there are no cases where two or more CNOTs are executed simultaneously. Thus, \(N_{CNOT}=1\). In addition, because three T gates are used simultaneously in the Toffoli gate, and because there are no cases where the Toffoli gate is used simultaneously in the entire algorithm, the maximum number of T gates used simultaneously throughout the algorithm is \(N_T=3\).
Slight modifications to the Roetteler algorithm
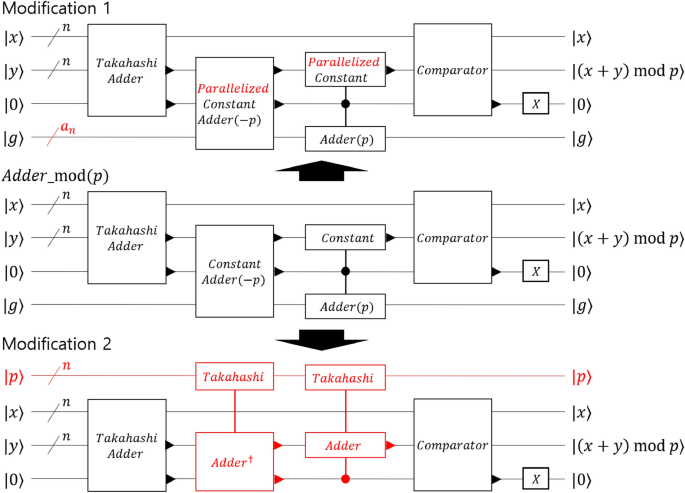
In this section, we modify the execution method of the constant adder in the RA and evaluate the change in the elementary gate step and T depth. As a constant adder is used throughout the RA, a little change in the constant adder causes a significant results. First, to reduce the required time for the algorithm, we replace Hänerâs serial version constant adder with a parallel one. As the parallel constant adder performs operations simultaneously, the elementary gate step and T depth can be reduced, but the \(N_{CNOT}\) and \(N_T\) increases. Second, we modify the constant adder that adds or subtracts a modular number p to a Takahashi adder by additionally using n logical qubits. These additional logical qubits are used to store modular number p as a quantum state. We do not change all constant adders used in the RA but change only the constant adders that add or subtract the modular number p to Takahashi adders. As the Takahashi adder has fewer elementary gate steps than the constant adder, it also shortens the required time.
Constant adder parallelization
Häner et al. also presented a method to parallelize the constant adder by additionally using dirty ancilla qubits in article32. Because this method additionally uses dirty ancilla qubits, it has the advantage of not having additional logical data qubits used for parallelization while reducing the elementary gate step and T depth. However, when the constant adder is parallelized, \(N_{CNOT}\) and \(N_T\) increase, and additional logical qubits for performing CNOT gate and magic-state factories are required. We used parallel constant adder to reduce the time required for the algorithm, even if we risk an increase in the number of physical qubits. Let us define the number of Toffoli gates that are used simultaneously as \(a_n\) and the number of CNOT gates that are used simultaneously as \(b_n\) when performing an n-bit quantum constant adder. As the constant adder has the form of divide-and-conquer, the n-bit constant adder is expressed as the sum of the constant adders of the upper and lower half bits. Therefore, \(a_n\) and \(b_n\) follow the recurrence relation
$$\begin{aligned} a_{n}=a_{\lceil \frac{n}{2} \rceil }+a_{\lfloor \frac{n}{2}\rfloor },~ b_{n}=b_{\lceil \frac{n}{2} \rceil }+b_{\lfloor \frac{n}{2}\rfloor }, \end{aligned}$$
(8)
where the natural number \(n\ge 2\) and \(a_1=0, a_2=0,a_3=1, a_4=1\) and \(b_1=0, b_2=1\). Although \(a_n\) and \(b_n\) cannot be expressed in a closed form, \(a_n\) and \(b_n\) for any n can be obtained using the values of \(a_1, a_2,a_3, a_4\), and \(b_1, b_2\). For example, when \(n=13\), \(a_{13}=a_7+a_6=(a_4+a_3)+(a_3+a_3)=4\) and \(b_{13}=b_7+b_6=b_4+3b_3=(b_2+b_2)+3(b_2+b_1)=5\). Using \(a_n\) and \(b_n\), when the bit length is n, \(N_{CNOT}\) and \(N_T\) can be expressed as
$$\begin{aligned} N_{CNOT}=b_n,~ N_{T}=3a_n. \end{aligned}$$
(9)
Using this modification, we can redefine the elementary gate step and depth of the parallelized constant adder RA. The elementary gate step \(Q_{Roe,parallel}\) and T depth \(D_{Roe,parallel}\) of the parallelized constant adder RA are expressed as follows (please see supplementary information).
$$\begin{aligned} Q_{Roe,parallel}&=19796n^3+3422n^2, \end{aligned}$$
(10)
$$\begin{aligned} D_{Roe,parallel}&=5100n^3+834n^2. \end{aligned}$$
(11)
Using Takahashi adder instead of constant adder
Although the n-bit constant adder uses only n logical qubits and thus requires fewer qubits than adder, which requires additional logical qubits, the elementary gate step and T depth of the constant adder are larger than those of the adder. For example, the Takahashi adder requires elementary gate step of 27n and T depth of 6n approximately, assuming CNOT gate serialization. Similarly, ripple-carry adder of Cuccaro et al.40, knwon as CDKM adder, requires an elementary gate step of 25n and a T depth of 6n approximately, assuming CNOT gate serialization again. Unlike the Takahashi adder, the CDKM adder requires one additional logical ancilla qubit. The Draper adder41 requires \(n+1\) steps of controlled rotation gate. However, The Draper adder requires approximate quantum Fourier transform(AQFT) before and after the operation and therefore requires an additional gate depth of \(O(n\log n)\). Furthermore, we have to approximate the rotation gate as H, S, and T gates using the Gridsynth algorithm42. For example, when the degree of approximation is \(10^{-10}\), a total of 253 H, S, and T gates are required and 102 T gates are required42. Therefore, Draper adder including AQFT was not considered in this paper because both the number of qubits used and the depth were larger than constant adder. Comparing the Takahashi adder and the CDKM adder, the CDKM adder has a slight advantage in terms of elementary gate steps compared to the Takahashi adder, but the T depth, which greatly affects the time required, is the same as Takahashi, and it uses one more logical qubit. In addition, when multiple-controlled adders are needed, such as modular inversion, Takahashi adders are more advantageous than CDKM adders. Therefore, when performing resource analysis, when comparing the method of replacing the constant adder with Takahashi adder and the method of replacing it with CDKM adder, the method using Takahashi adder uses slightly fewer physical qubits and takes the same amount of time (please see supplementary information). Therefore, we replaced constant adder with Takahashi adder. The disadvantage of the Takahashi adder is that the number to be added must be prepared in the quantum state. Therefore, we replaced only the constant adder for adding or subtracting the modular number p, which is frequently used in modular operations, with the Takahashi adder. Using this method, only n additional logical qubits must be generated to store modular number p.
As in the RA, it is assumed that the CNOT gates are serially performed on Takahashi adder to minimize \(N_{CNOT}\). Therefore, as in the RA, \(N_{CNOT}=1\) and \(N_T=3\).
The elementary gate step \(Q_{Roe,T}\) and T depth \(D_{Roe,T}\) of the Takahashi adder version RA are expressed as follows (please see supplementary information).
$$\begin{aligned} Q_{Roe,T}&=15776^3 + 824n^2\log _2 n -804n^2,\end{aligned}$$
(12)
$$\begin{aligned} D_{Roe,T}&=4056n^3 + 192n^2\log _2 n -180n^2. \end{aligned}$$
(13)

Wanda Parisien is a computing expert who navigates the vast landscape of hardware and software. With a focus on computer technology, software development, and industry trends, Wanda delivers informative content, tutorials, and analyses to keep readers updated on the latest in the world of computing.