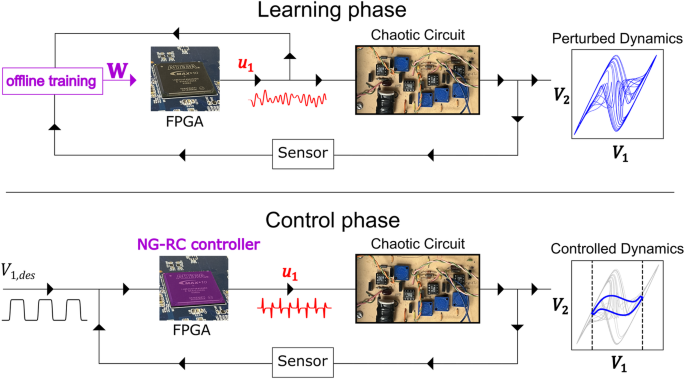
An overview of our prototype chaotic circuit and nonlinear control system is shown in Fig. 1. The chaotic circuit (known as the “plant” in the control literature) consists of passive components including diodes, capacitors, resistors, and inductors, and an active negative resistor realized with an operational amplifier that can source and sink power to the rest of the circuit. The phase space of the system is three-dimensional specified by voltages V1 and V2 across two capacitors in the circuit and the current I passing through the inductor (see Methods). To display chaos, the circuit must be nonlinear, which arises from the diodes as evident from their nonlinear current-voltage relation. We adjust the circuit parameters so that it displays autonomous double-scroll chaotic dynamics characterized by a positive Lyapunov exponent, indicating chaotic dynamics16. A two-dimensional projection of the phase space trajectory allows us to visualize the corresponding strange attractor and is show in Fig. 1.
(top) Learning phase. A field programmable gate array (FPGA) applies perturbations (red) to a chaotic circuit and the perturbed dynamics of the circuit (blue) are measured by a sensor (analog-to-digital converters). The temporal evolution of the perturbations and responses are transferred to a personal computer (left, purple) to learn the parameters of the NG-RC controller \({{{{{\bf{W}}}}}}\). These parameters are programmed onto the FPGA as well as the firmware for the controller. (bottom) Control phase. The NG-RC controller implemented on the FPGA measures the dynamics of the chaotic circuit with a sensor (analog-to-digital converters) in real time and receives a desired trajectory \({V}_{1,{des}}\) for the \({V}_{1}\) variable, and computes a suitable control signal (red) that drives the circuit to the desired trajectory.
To control the system, we measure in real time two accessible variables – voltages V1 and V2 – using analog-to-digital converters located on the FPGA (the sensors indicated in Fig. 1). We are limited to measuring two variables because of the available resources on the device. For a similar reason, we are limited to controlling a single variable, which we take as V1 based on previous control experiments with this circuit16. Here, the user provides a desired value V1,des as the control target, which can be time-dependent.
The goal of the controller is to guide the system to the desired state by perturbing its dynamics based on a nonlinear control law. Controlling this system to a wide range of behaviors requires that the controller also be nonlinear; the applied perturbations are a nonlinear function of the measured state variables. Importantly, a nonlinear controller allows us to go beyond established chaos control methods that are restricted to controlling about sets embedded in the dynamics and only applying control when the system is close to one of these sets4,17,18, as mentioned above.
Coming back to the control implementation, we use two phases: (1) a learning phase where we learn the dynamics of the chaotic circuit and how it responds to random perturbations (Fig. 1, top panel) in an “open” configuration; and (2) a closed-loop configuration (Fig. 1, bottom panel), where the learned model generates perturbations based on the real-time measurements and the user-specified desired state. We store the desired state in local on-chip memory to reduce the system power consumption, but it is straightforward to interface our controller with a higher-level system manager or user interface to allow greater flexibility.
During the training phase, we synthesize a low-pass-filtered random sequence and store it in on-chip memory (see Methods). This sequence is read out of memory and sent off-chip to a digital-to-analog converter, which passes to a custom-built voltage-to-current converter (u1 in the top panel of Fig. 1, red waveform) and injected into the chaotic circuit at the node corresponding to the capacitor giving rise to voltage V1.
The control current perturbs the chaotic dynamics so we can learn how it responds to perturbations at many locations in phase space, which is common in extremum-seeking control19, for example. To this end, we simultaneously measure the voltages V1 and V2 and store their values in on-chip memory. After a training session, the data is transferred to a laptop computer to determine the NG-RC model as described below. The model is then programmed in the FPGA logic.
Nonlinear control is turned on by “closing the loop.” Here, the real-time measured voltages and the desired state are processed by the NG-RC model, control perturbations calculated, and subsequently injected into the circuit. There is always some latency between measurements and perturbation, which can destabilize the control if it becomes comparable to or larger than the Lyaponov time – the interval over which chaos causes signal decorrelation20. We optimize the overall system timing to minimize the latency, but the NG-RC model and control law is so simple that the evaluation time is two orders of magnitude shorter than the other latencies present in the controller, which are detailed Supplementary Note 7. Another important aspect of our controller is that we use fixed-point arithmetic, which is matched to the digitized input data and reduces the required compute resources and power consumption10.
Control law
We formalize the control problem as follows: the accessible variables of the chaotic circuit \({{{{{\bf{X}}}}}}{{\in }}{{\mathbb{R}}}^{{d}^{{\prime} }}\) are the inputs to a nonlinear control law that specifies the control perturbations \({{{{{\bf{u}}}}}}{{\in }}{{\mathbb{R}}}^{{{{{{\boldsymbol{d}}}}}}}(d\le {d{{\hbox{‘}}}})\) necessary to guide a subset of the accessible system variables \({{{{{\bf{Y}}}}}}{{\in }}{{\mathbb{R}}}^{d}\) to a desired state \({{{{{{\bf{Y}}}}}}}_{{des}}{{\in }}{{\mathbb{R}}}^{d}\). We assume the dynamics of the system evolve in continuous time, but discretely sampled data allows us to describe the dynamics of the uncontrolled system in the absence of noise by the mapping
$${{{{{{\bf{X}}}}}}}_{i+m}={{{{{{\bf{F{{\hbox{‘}}}}}}}}}}_{i+m}\left({{{{{{\bf{X}}}}}}}_{i},\, {{{{{{\bf{X}}}}}}}_{i-1},\ldots,\, {{{{{{\bf{X}}}}}}}_{i-\left(k-1\right)}\right),$$
(1)
where \(i\) represents the index of the variables at time \({t}_{i}\), \(m\) is the number of timesteps the map projects into the future and \({{{{{{\bf{F{{\hbox{‘}}}}}}}}}}_{i+m}{{\in }}{{\mathbb{R}}}^{{d}^{{\prime} }}\) is a nonlinear function specifying the flow of the system, which may depend on k past values of the system variables. The dynamics of the controlled variables are then given by \({{{{{{\bf{Y}}}}}}}_{i+m}={{{{{{\bf{F}}}}}}}_{i+m}\), where \({{{{{{\bf{F}}}}}}}_{i+m}{{\in }}{{\mathbb{R}}}^{d}\) is related to \({{{{{{\bf{F{{\hbox{‘}}}}}}}}}}_{i+m}\) through a projection operator. We assume the control perturbations at time \({t}_{i}\) affect the dynamics linearly, while past values may have nonlinear effects on the flow of the system, allowing us to express the dynamics of the controlled system variables as
$${{{{{{\bf{Y}}}}}}}_{i+m}={{{{{{\bf{F}}}}}}}_{i+m}\left({{{{{{\bf{X}}}}}}}_{i},\, {{{{{{\bf{X}}}}}}}_{i-1},\ldots,\, {{{{{{\bf{X}}}}}}}_{i-\left(k-1\right)},\, {{{{{{\bf{u}}}}}}}_{i-1},\ldots,\, {{{{{{\bf{u}}}}}}}_{i-(k-1)}\right)+\, {{{{{{\bf{W}}}}}}}_{u}{{{{{{\bf{u}}}}}}}_{i},$$
(2)
where we omit the arguments of \({{{{{{\bf{F}}}}}}}_{i+m}\) below for brevity.
To control a dynamical system of the form (2), we use a general nonlinear control algorithm developed for discrete-time systems21. Different from many previous nonlinear controllers22, we do not require a physics-based model of the plant. Rather, we use a data-driven model learned during the training phase. Robust and stable control of the dynamical system is obtained21,23 by taking
$${{{{{{\bf{u}}}}}}}_{i}={\hat{{{{{{\bf{W}}}}}}}}_{u}^{-1}\left[{{{{{{\bf{Y}}}}}}}_{{des},i+m}-{\hat{{{{{{\bf{F}}}}}}}}_{i+m}+{{{{{\bf{K}}}}}}{{{{{{\bf{e}}}}}}}_{i}\right],$$
(3)
where, \({{{{{{\bf{Y}}}}}}}_{{des},i+m}{{\in }}{{\mathbb{R}}}^{d}\) is the desired state of the system m-steps-ahead in the future, \({{{{{\bf{K}}}}}}{{\in }}{{\mathbb{R}}}^{d\times d}\) is a closed loop gain matrix, and \({{{{{{\bf{e}}}}}}}_{i}={{{{{{\bf{Y}}}}}}}_{i}-{{{{{{\bf{Y}}}}}}}_{{des},i}\) is the tracking error. The ″^″ over the symbols indicate that these quantities are learned during the training phase using the procedure described in the next subsection. A key assumption is that we can learn \({{{{{{\bf{F}}}}}}}_{i+m}\) only using information from the accessible system variables and past perturbations.
The control law (3) executes feedback linearization, where the feedback attempts to cancel the nonlinear function \({{{{{{\bf{F}}}}}}}_{i+m}\) in mapping (2), thus reducing to a linear control problem. To see this, assume perfect learning (\({\hat{{{{{{\bf{F}}}}}}}}_{i+m}={{{{{{\bf{F}}}}}}}_{i+m}\), \({\hat{{{{{{\bf{W}}}}}}}}_{u}=\)\({{{{{{\bf{W}}}}}}}_{u} \left)\right.\), and apply the definition of the tracking error to obtain
$${{{{{{\bf{e}}}}}}}_{i+1}={{{{{\bf{K}}}}}}{{{{{{\bf{e}}}}}}}_{i}.$$
(4)
This system is globally stable when all eigenvalues of \({{{{{\bf{K}}}}}}\) are within the unit circle. Adjustments to \({{{{{\bf{K}}}}}}\) are required to maintain globally stable control in the presence of bounded modeling error and noise21.
For comparison, we compare our nonlinear controller to a simple linear proportional feedback controller. We can make a simple adjustment to the control law described above to realize a linear controller. Consider the case when the sampling time \({{{{{\boldsymbol{\triangle }}}}}}{{{{{\rm{t}}}}}}\) is short relative to the timescale of the system’s dynamics, allowing us to approximate the flow \({\hat{{{{{{\bf{F}}}}}}}}_{i+m}\) in the control law (3) with the current state \({{{{{{\bf{Y}}}}}}}_{i}\) to arrive at a linear control law. This is motivated by approximating the flow using Euler integration with a single step \({{{{{{\bf{Y}}}}}}}_{i+1} \, \approx \, {{{{{{\bf{Y}}}}}}}_{i}{{{{{\boldsymbol{+}}}}}}{{{{{\boldsymbol{\triangle }}}}}}{{{{{\rm{t}}}}}}{{{{{\bf{f}}}}}}\left({t}_{i},\, {{{{{{\bf{X}}}}}}}_{i}\right)\), where \({{{{{\bf{f}}}}}}\left({t}_{i},\, {{{{{{\bf{X}}}}}}}_{i}\right)\) is the vector field governing the dynamics, and observing that \({{{{{{\bf{Y}}}}}}}_{i+1} \, \approx \, {{{{{{\bf{Y}}}}}}}_{i}\) when \({{{{{\boldsymbol{\triangle }}}}}}{{{{{\rm{t}}}}}}\) approaches zero.
Based on the number of accessible system variables and control perturbations in our system, we take \({d}^{{\prime} }=2\) and d = 1 corresponding to \({{{{{{\bf{X}}}}}}}_{i}={\left[{V}_{1,i},{V}_{2,i}\right]}^{T}\), \({{{{{{\bf{Y}}}}}}}_{i}={V}_{1,i}\), \({{{{{{\bf{u}}}}}}}_{i}={u}_{1,i}\), and the feedback control gain K is a scalar. Additionally, we take \(m=1\) (2) in this work for one-step- (two-step-) ahead prediction, as this provides a trade-off between controller stability and accuracy.
Reservoir computing
Here, we briefly summarize the NG-RC algorithm12,13 used to estimate \({\hat{{{{{{\bf{W}}}}}}}}_{u}^{-1}\) and \(\hat{{{{{{\bf{F}}}}}}}\) needed for the control law. Like most ML algorithms, an RC maps input signals into a high-dimensional space to increase computational capacity, and then projects the system onto the desired low-dimensional output. Different from other popular ML algorithms, RCs have natural fading memory, making them particularly effective at learning the behavior of dynamical systems.
A RC gains much of its strength by using a linear-in-the-unknown-parameters universal representation24 for \(\hat{{{{{{\bf{F}}}}}}},\) which vastly simplifies the learning process that uses linear regularized least-squares optimization. The other strength is that the number of trainable parameters in the model is smaller than other popular ML algorithms, thus reducing the size of the training dataset and the compute time for training and deployment. Previous studies have successfully used an RC to control a robotic arm25 and a chaotic circuit14, for example, using an inverse-control method26.
The next-generation reservoir computing algorithm has similar characteristics to a traditional RC27, but has fewer parameters to optimize, requires less training data, and is less computationally expensive15. In this framework, the function \(\hat{{{{{{\bf{F}}}}}}}\) is represented by a linear superposition of nonlinear functions of the accessible system variables \({{{{{\bf{X}}}}}}\) at the current and past times, as well as perturbations \({{{{{\bf{u}}}}}}\) at past times, as mentioned previously. The number of time-delayed copies k of these variables form the memory of the NG-RC. Based on previous work on learning the double-scroll attractor15, we use k = 2 and use odd-order polynomial functions of \({{{{{\bf{X}}}}}}\) up to cubic order, but we only take linear functions of past perturbations \({{{{{{\bf{u}}}}}}}_{i-1}\) for simplicity. The feature vector also contains the perturbations \({{{{{{\bf{u}}}}}}}_{i}\), which allows us to estimate \({\widehat{{{{{{\bf{W}}}}}}}}_{u}\). We perform system identification28,29 to select the most important components of the model. Additional details regarding the NG-RC implementation are given in the Methods.
Control tasks
We apply our nonlinear control algorithm with three challenging tasks. The first is to control the system to the unstable steady state (USS) located at the origin [V1 = 0, V2 = 0, I = 0] of phase space starting from a random point located on the strange attractor. Previous work by Chang et al.16 fail to stabilize the system at the origin using an extended version of the Pyragas approach30.
The second task is to control the system about one of the USSs in the middle of one of the “scrolls” and then guide the system to the USS at the other scroll and then back in rapid succession. Rapid switching between these USSs is unattainable using Pyragas-like approaches because the controller must wait for the system to cross into the opposite basin of attraction defined by the line V1 = 016, which cannot occur within the requested transition time. Additionally, the system never visits the vicinity of these USSs16 and hence large perturbations are required to perform the fast transitions, causing the OGY4 approach to fail.
Last, we control the system to a random trajectory, which determines if the system can be controlled to an arbitrary time-dependent state. This task is difficult because the controller must cancel the nonlinear dynamics at all points in phase space, requiring an accurate model of the flow. This task is infeasible for Pyragas-like approaches, as they are limited to controlling the system to UPOs and USSs. There are extensions of the OGY method that can steer the system to arbitrary points on the attractor31, but controlling between arbitrary points quickly requires large perturbations, making this approach unsuitable. Furthermore, this approach can require significant memory to store paths to the desired state32, increasing the power and resource consumption.
Example trajectories
Example phase-space trajectories of the controlled system for the three different tasks are shown in Fig. 2. For the first, the dynamics of the system are far from the origin when the controller is turned on (indicated by an × in the phase portrait) and quickly evolves toward the origin and remains stable for the remainder of the control phase. Note that we only control \({V}_{1}\); \({V}_{2}\) and I (not shown) are naturally guided to zero through their coupling to V1.
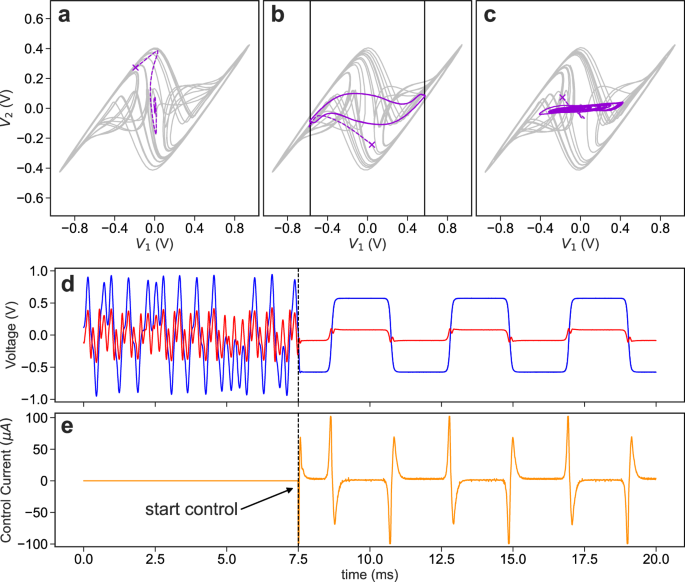
Controlled attractors for a the first task controlling the system to the origin, b controlling back and forth between the two USSs (solid black), and c controlling to a random waveform. The unperturbed attractor (gray) before the control is switched on, the moment the control is switched on (purple ×), the transient for the system to reach the desired trajectory (dashed purple), and the controlled system (solid purple). d Temporal evolution of \({V}_{1}\) (blue), and \({V}_{2}\) (red) during the second task. When the control begins, the chaotic system follows the desired trajectory (solid black), which is under the blue curve. e The control perturbation before and after the control is switched on (orange). The control gain is set to K = 0.75 for all cases.
For the second task, it is seen that \({V}_{1}\) and \({V}_{2}\) are successfully guided to the corresponding values of the USSs. The trajectory followed by the system as it transitions between the USSs depends on the requested transition rate because changes in V2 lags changes in V1 as governed by their nonlinear coupling. The temporal evolution of the system is shown in Fig. 2d, e, where we see that \({V}_{1}\) accurately follows the desired trajectory without any visible overshoot.
For the final task, we request that V1 follows a random trajectory contained within the domain of the strange attractor as shown in Fig. 2c; additional results visualizing the controlled system is given in Supplementary Note 2.
Control performance
We now characterize the stability of the nonlinear controller as a function of the feedback gain K and compare the control error on the three tasks for the linear and nonlinear controllers. Figure 3 shows the performance of the controller as K varies, where Fig. 3a shows the error between the requested and actual state of the system, while Fig. 3b shows the size of the control perturbations. We see that there is a broad range of feedback gains that give rise to high-quality control, and the control perturbations are small at the USSs, showing the robustness of our approach. The domain of control is somewhat smaller than that expected, which we believe is due to small modeling errors and latency between measuring the state and applying the control perturbation20,33. We find that the NG-RC controller with two-step-ahead prediction has a substantially larger domain of control, which is detailed in Supplementary Note 3.
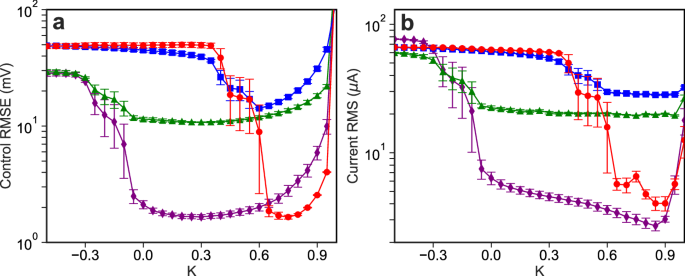
a RMSE of the control and b RMS of the control current when controlling the system to the phase-space origin (red circles), back-and-forth between two USSs (green triangles), to a random waveform (blue squares), and stabilized at either nonzero USS (purple diamonds) as a function of the control gain \(K\).
The minimum error for each task and controller type is given in Table 1. We see that the NG-RC controllers outperforms the linear controller on every task, except when the system is stabilized at the nonzero USSs because the dynamics are approximately linear there.
The advantage of the NG-RC controller is evident for the random waveform task, where we observe a 1.7\(\times\) reduction in the error compared to the linear controller. This task is especially challenging for the linear controller because the desired state visits a wide range of phase space with different local linear dynamics and the sampling rate is too slow for \({{{{{{\bf{Y}}}}}}}_{i+1} \, \approx \, {{{{{{\bf{Y}}}}}}}_{i}\) to be a good approximation, making the controller ineffective at canceling the nonlinear dynamics of the system. Additional performance metrics, such as the error, size of control perturbations, and sensitivity to control-loop latency are given in the Supplementary Note 3.
Control resources
We now discuss the resources needed for implementing control. First, the FPGA demonstration board has resources well matched to the chaotic system. The characteristic timescale of the chaotic circuit is 24 \({{{{{\rm{\mu }}}}}}{{{{{\rm{s}}}}}}\), which compares favorably with the 1 Msample/s sampling rate of the analog-to-digital and digital-to-analog converters and our control update period of 5 μs. Unlike previous ML-based controllers, the update period is not limited by the evaluation time of the ML model and control law, which only requires a computation time of 50 ns.
Regarding power consumption, our demonstration board is not designed for low-power operation and there is a substantial power-on penalty when using the board. For the NG-RC-based controllers, we observe a total power consumption of 1384.0 \(\pm\) 0.7 mW, where 53\(.5\pm\) 1.4 mW is consumed by the analog-to-digital and digital-to-analog converters, 5.0 \(\pm\) 1.4 mW is consumed evaluating the NG-RC algorithm, and the remainder is for other on-board devices not used directly by the control algorithm. Considering the control loop rate of 200 kHz, these results indicate that we only expend 25.0 \(\pm\) 7.0 nJ per inference if we consider only the energy consumed by the NG-RC, or 6920\(.0\pm\) 3.5 nJ considering the total power. In contrast, the linear controller requires only 7.5 \(\pm\) 7.0 nJ per inference, which is primarily due to the decreased number of multiplications.
Regarding the logic and math resources on the FPGA, the one-step ahead controller uses 1722 logic elements (3% of the available resources), 924 registers (1.8%), and 18 multipliers (13%). The two-step ahead controller requires 16 additional registers to store the desired state two steps in the future, but otherwise uses the same resources. In contrast, the linear controller uses 986 (2%) logic elements, 604 registers (1.2%), and 4 multipliers. All controllers use only 768 memory bits (< 1%) for the origin task, which does not require any additional memory to store the desired signal. These resources are small in comparison to other recent ML-based control algorithms evaluated on an FPGA, which we present in Supplementary Note 4. Additionally, we show that the computational complexity of our approach is significantly lower than the RC-based inverse controller by Canaday et al.14 in Supplementary Note 1.

Wanda Parisien is a computing expert who navigates the vast landscape of hardware and software. With a focus on computer technology, software development, and industry trends, Wanda delivers informative content, tutorials, and analyses to keep readers updated on the latest in the world of computing.