AGV scheduling problems have many classifications according to different scenarios and considerations. For example, consider the time window of the task, joint optimization of scheduling and path, cooperation with other devices, charging strategy and so on. Due to the limitation of quantum bits of CIM, it is impossible to solve the AGV scheduling problem in complex scenes27,28,29. Therefore, we simplify the problem and keep the essence of AGV scheduling problem. On this basis, we construct the AGV scheduling model. In this section, we present the classical AGV scheduling model based on mixed integer programming (MIP), and propose two new models, which we call the node and arc models.
Problem description
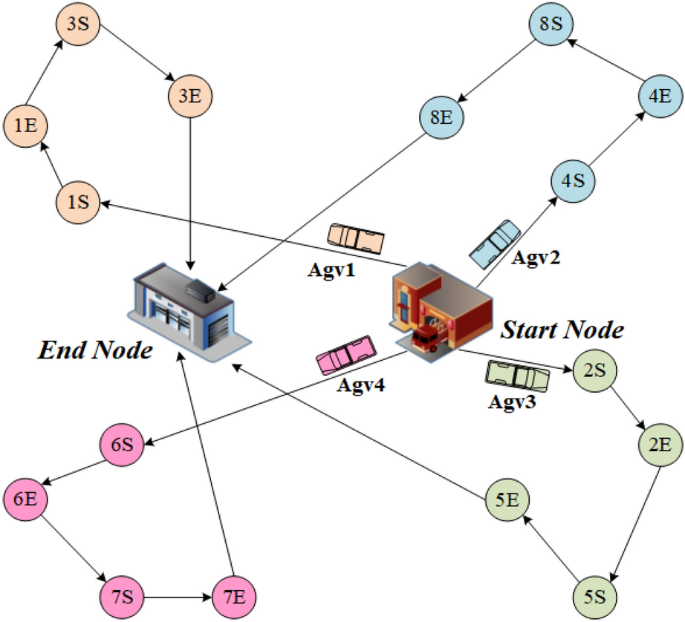
The AGV scheduling problem and a feasible solution. All AGVs start from a fixed start node, perform transportation tasks, and reach the end node after performing all tasks. ’S’ represents the starting point of a transportation task, and ’E’ represents the end point of a transportation task. Different colors represent different AGV’s mission routes.
We consider an AGV scheduling problem (to make the problem more general, we do not set up a working scenario), as shown in Fig. 1. Given an AGV set, all AGVs have a unified starting node and ending node, and all AGVs start to accept tasks from the unified starting node until all transportation tasks are completed, and then return to the unified ending node. In the AGV scheduling problem, we are given a set of transportation tasks, each with a starting point and an ending point. For an AGV, the process of completing the transportation task can be described as first arriving at the starting point of the task to load the transported goods, then transporting them to the ending point of the task, and then driving to the starting point of the next task to perform the next task. The travel time of the AGV between any two task points is known. We consider two optimization objectives, the first is to minimize the total AGV travel time and the second is to minimize the maximum task completion time (makespan). The first objective is generally used when the task is not urgent to achieve a reduction in total system energy consumption, while the second objective is set to complete transportation tasks quickly.
Next, we elaborate on the symbolic settings in the problem as follows.
\(V=\{1,\ldots ,k,\ldots ,K \}\) set of AGVs,
\( R=\{1,\ldots ,r,{{r}^{‘}},{{r}^{”}},\ldots ,n-1 \}\) set of actual tasks,
\({{R}_{1}}=\{0,1,\ldots ,r,{{r}^{‘}},{{r}^{”}},\ldots ,n-1\}\) set of actual tasks and virtual start task,
\({{R}_{2}}=\{1,\ldots ,r,{{r}^{‘}},{{r}^{”}},\ldots ,n\}\) set of actual tasks and virtual end task,
\({{R}^{‘}}=\{0,1,\ldots ,r,{{r}^{‘}},{{r}^{”}},\ldots ,n\}\) set of all tasks,
\(A=\{(r,{{r}^{‘}})\mid r,{{r}^{‘}}\in {{R}^{‘}}\}\) arc set that consists of all valid task pairs that can be conducted adjacently,
\(\pi =\{1,\ldots ,t,\ldots ,N \}\) set of the sequence of tasks performed by an AGV
a a single task arc
\(\theta _{r}^{+}\) an arc with task r as the left node
\(\theta _{r}^{-}\) an arc with task r as the right node
\(r_{\text{s}}\) starting point of task r,
\(r_{\text{d}}\) ending point of task r.
\({{e}_{{{r}_\text{s}}{{r}_\text{d}}}}\) indicates the travel time of the AGV from two points \({{r}_\text{s}}\) and \({{r}_\text{d}}\),
\({{e}_{{{r}_\text{d}}r_\text{s}^{‘}}}\) indicates the travel time of the AGV from two points \({{r}_\text{d}}\) and \(r_\text{s}^{‘}\),
\({{c}_{r{{r}^{‘}}}}\) contains two parts of time, the first part is the time from the start of task r to the end of task r, and the second part is the time from the end of task r to the start of task \({r}^{‘}\), \({{c}_{r{{r}^{‘}}}}={{e}_{{{r}_{s}}{{r}_{d}}}}+{{e}_{{{r}_{d}}r_{s}^{‘}}}\).
Mixed integer programming model
In this subsection, we introduce the classical model of AGV scheduling. The classical model is formed as a mixed integer programming, and it has the following variables.
\({{y}_{r,{{r}^{‘}},k}}\) binary variable, equal to 1 if task r is performed directly prior to \({{r}^{‘}}\) by AGV k, 0 otherwise;
\(f^\text{s}_{rk}\) arrival time of AGV k at the start node of task r;
\(f^\text{d}_{rk}\) arrival time of AGV k at the end node of task r;
T the makespan for AGVs to perform transportation tasks.
The first optimization objective of the MIP model is to minimize the total AGV travel time, and its model is presented as follows.
$$\begin{aligned} \text {(P1)}\qquad&\text {min}{} & {} \sum _{k\in V} f_{nk}^\text{d} \end{aligned}$$
(1)
$$\begin{aligned}&\text {s.t.}{} & {} \sum _{r’\in R_2} y_{0,r’,k}=1&\forall k\in V \end{aligned}$$
(2)
$$\begin{aligned}{} & {} {}&\sum _{r\in R_1}y_{r,n,k}=1&\forall k\in V \end{aligned}$$
(3)
$$\begin{aligned}{} & {} {}&\sum _{r’\in R_2}\sum _{k\in V} y_{r,r’,k}=1&\forall r\in R \end{aligned}$$
(4)
$$\begin{aligned}{} & {} {}&\sum _{r’\in R_1}y_{r’,r,k}-\sum _{r’\in R_2} y_{r,r’,k}=0&\forall r\in R,\forall k\in V \end{aligned}$$
(5)
$$\begin{aligned}{} & {} {}&f_{0k}^\text{s}=f_{0k}^\text{d}=0&\forall k\in V \end{aligned}$$
(6)
$$\begin{aligned}{} & {} {}&f_{rk}^\text{s}+e_{r_\text{s}r_\text{d}}=f_{rk}^\text{d}&\forall k\in V, \forall r\in R’ \end{aligned}$$
(7)
$$\begin{aligned}{} & {} {}&f_{rk}^\text{d}+e_{r_\text{d}r’_\text{s}}\le f_{r’k}^\text{s}+M(1-y_{r,r’,k})&\forall r,r’\in R,\forall k\in V \end{aligned}$$
(8)
$$\begin{aligned}{} & {} {}&y_{r,r,k}=0&\forall r\in R,\forall k\in V \end{aligned}$$
(9)
$$\begin{aligned}{} & {} {}&{{y}_{r,{{r}^{‘}},k}}\in \{0,1\}\text { }&\forall {r,}{{{r}}^{‘}}\in {{R}^{‘}},\forall k\in V \end{aligned}$$
(10)
$$\begin{aligned}{} & {} {}&f_{rk}^{s},f_{rk}^{d}\ge 0\text { }&\forall {r}\in {R,}\forall {k}\in {V}. \end{aligned}$$
(11)
The objective function (1) is to minimize the total travel time of the AGV. Constraints (2) and (3) ensure that all AGVs need to complete the virtual start task and the virtual end task, and constraints (4) guarantee that all actual tasks are uniquely assigned to a particular AGV. Constraints (5) ensure that each AGV completes its task satisfying the flow balance. Then, constraints (6) guarantee that the virtual start task starts and ends at moment 0. Constraints (7) states that the time to reach the end of a task is equal to the time to reach the start of that task plus the transport time from the start to the end. Constraints (8) indicates that the time to reach the start of a task is later than the time to reach the end of the previous task plus the transportation time required to reach the start of that task from the end of the previous task, where M is a sufficiently large value. The last constraints (9) eliminates task self-citation. Constraints (10) and (11) represent range limits of variables.
A slight modification of the above model can be used as a model for minimizing the makespan for AGVs to perform transportation tasks, which is given as follows, Eqs. (2)–(11).
$$\begin{aligned} \text {(P2)}\qquad&\text {min}{} & {} T \end{aligned}$$
(12)
$$\begin{aligned}&\text {s.t.}{} & {} T\ge f_{nk}^{d}&\forall k\in V. \end{aligned}$$
(13)
where T denotes the makespan. The objective function is to minimize T, and constraints (13) denotes that T must be no less than the time required by the last AGV to complete the task.
QUBO model
QUBO and Ising model
This section mainly describes the concepts of QUBO model and Ising model and their relationship. QUBO is an expression of optimization problem, and its goal is to find binary variables that minimize quadratic polynomials. Ising model was first put forward and applied in statistical physics. It describes a system composed of interacting units, in which each spin particle must have two possible random states (such as + 1 and − 1), and then it was introduced into the field of mathematics as a model to describe a series of optimization problems. Many combinatorial optimization problems can be expressed in the form of quadratic unconstrained binary optimization or ising model, and they can be transformed into each other30,31,32. The general expression of QUBO model is shown in Eq. (14).
$$\begin{aligned} H(x)={{x}^\texttt{T}}Qx+{{c}^\texttt{T}}x,x\in {{\{0,1\}}^{z}} \end{aligned}$$
(14)
where x is a z dimensional vector of binary variables, Q is the quadratic coefficient matrix, and \({{c}^\texttt{T}}\) is the coefficient matrix of the primary term.
The above model in the form of QUBO can be easily transformed into an Ising model, and the variable range of the Ising model is \(\left\{ -1,1 \right\} \). Specifically, it can be realized by variable substitution \({{\sigma }_{i}}=2{{x}_{i}}-1\). Then, the optimization function can be expressed in the following form.
$$\begin{aligned} H(\sigma )=-\sum \limits _{i,j}{{{J}_{ij}}}{{\sigma }_{i}}{{\sigma }_{j}}-\sum \limits _{i}{{{h}_{i}}}{{\sigma }_{i}} \end{aligned}$$
(15)
where the \({{\sigma }_{i}}\) is spin variable, \({{J}_{ij}}\) and \({{h}_{i}}\) are the quadratic and linear coefficients. The solution of Ising problem is to find the ground state of Hamiltonian. CIM solves the Ising problem according to the principle of minimum gain, and can find the ground state or low energy state of Ising Hamiltonian. The method is to map the QUBO problem into a fully connected Ising Hamiltonian with programmable parameters, and obtain the solution of the problem through controllable quantum phase transition33,34.
Node model
In this section, we will describe the node model. The core idea of node model is to regard tasks as nodes and the order of task execution as the order of vehicles passing through nodes.The node model has the QUBO form and is suitable for quantum computing, the variables of the model are described as below.
\({{x}_{r,t,k}}\) binary variable, equal to 1 if task r is assigned to AGV k as it is t-th task, 0 otherwise.
The first optimization objective of the node model is to minimize the total AGV travel time, and the model is shown below.
$$\begin{aligned} \text {(P3)}\qquad {{H}_{1}}&={{\partial }_{1}}{{H}_{A}}+{{\partial }_{2}}{{H}_{B}}+{{\partial }_{3}}{{H}_{C}}+{{\partial }_{4}}{{H}_{D}}+{{\partial }_{5}}{{H}_{E}}+{{\partial }_{6}}{{H}_{F}} \end{aligned}$$
(16)
$$\begin{aligned} {{H}_{A}}&=\sum \limits _{k\in V}{\sum \limits _{(r,{{r}^{‘}})\in A}{\sum \limits _{t=1}^{N-1}{{{c}_{r{{r}^{‘}}}}}}}{{x}_{r,t,k}}{{x}_{{{r}^{‘}},t+1,k}} \end{aligned}$$
(17)
$$\begin{aligned} {{H}_{B}}&={{\sum \limits _{k\in V}{(1-{{x}_{0,1,k}})}}^{2}}\ \end{aligned}$$
(18)
$$\begin{aligned} {{H}_{C}}&=\sum \limits _{k\in V}{\sum \limits _{r\in R}{\sum \limits _{t=2}^{N-1}{{{x}_{n,t,k}}}}}{{x}_{r,t+1,k}} \end{aligned}$$
(19)
$$\begin{aligned} {{H}_{D}}&=\sum \limits _{r\in R}{{{\left( 1-\sum \limits _{k\in V}{\sum \limits _{t=2}^{N-1}{{{x}_{r,t,k}}}}\right) }^{2}}} \end{aligned}$$
(20)
$$\begin{aligned} {{H}_{E}}&=\sum \limits _{k\in V}{\sum \limits _{\begin{array}{c} r,{{r}^{‘}}\in {{R}^{‘}} \\ r\ne {{r}^{‘}} \end{array}}{\sum \limits _{t=1}^{N}{{{x}_{r,t,k}}{{x}_{{{r}^{‘}},t,k}}}}} \end{aligned}$$
(21)
$$\begin{aligned} {{H}_{F}}&=\sum \limits _{k\in V}{\sum \limits _{t=1}^{N-1}{{{\left( \sum \limits _{r\in {{R}_{1}}}{{{x}_{r,t,k}}}-\sum \limits _{{{r}^{‘}}\in {{R}_{2}}}{{{x}_{{{r}^{‘}},t+1,k}}}\right) }^{2}}}}.\ \end{aligned}$$
(22)
\({{\partial }_{i}}\) \((i=1,\ldots ,6)\) are weights correspond to each objective function. The objective function (17) is to minimize the total travel time of all the AGVs. The minimization function (18) and (19) ensures that for each AGV, the virtual start task and the virtual end task must be the first task and the last task, respectively. For each actual task, we want it to be assigned exactly to one AGV, so we add the minimization function (20). We also consider the minimization function (21) in order to make each AGV perform at most one task on each task sequence. For a particular AGV, the order of its tasks must be continuous, based on which we set the minimization function (22).
The model described below is modified from the above model to accommodate the goal of minimizing the makespan.
The least time-consuming task model requires finding the AGV with the longest task execution time and minimizing its execution task time, which leads to inequality constraints, as follows.
$$\begin{aligned}&T\ge \sum \limits _{(r,{{r}^{‘}})\in A}{\sum \limits _{t=1}^{N-1}{{{c}_{r{{r}^{‘}}}}}}{{x}_{r,t,k}}{{{x}_{{{r}^{‘}},t+1,k}}}\quad \forall k\in V \end{aligned}$$
(23)
$$\begin{aligned}&{{H}_{Y}}=T \end{aligned}$$
(24)
The objective function (24) is to minimize the makespan T.
Then we add slack variables to transform the above inequality constraint into an equation, as follows.
$$\begin{aligned}&{{H}_{Z}}={{\sum \limits _{k\in V}{\left( T-\sum \limits _{(r,{{r}^{‘}})\in A}{\sum \limits _{t=1}^{N-1}{{{c}_{r{{r}^{‘}}}}{{x}_{r,t,k}}{{x}_{{{r}^{‘}},t+1,k}}-{{T}_{k}}}}\right) }}^{2}} \end{aligned}$$
(25)
$$\begin{aligned}&{T=}{{\delta }_{1}}\text {+2}{{\delta }_{2}}\text {+}\ldots \text { +}{{\text {2}}^{m}}{{\delta }_{m}}\ \end{aligned}$$
(26)
$$\begin{aligned}&{{{T}}_{k}}{=}{{\delta }_{1k}}\text {+2}{{\delta }_{2k}}\text {+}\ldots \text { +}{{\text {2}}^{{{m}^{‘}}}}{{\delta }_{{{m}^{‘}}k}} \end{aligned}$$
(27)
\({{T}_{k}}\) \((k\in V)\) is the slack variable, and both T and \({{T}_{k}}\) \((k\in V)\) need to be represented by binary variables. \({{\delta }_{i}}\) \( (i=1,2,\ldots ,m)\) and \({{\delta }_{ik}}\) \((i=1,2,\ldots ,{m}^{‘}, {k}\in {V})\) are the discretized auxiliary variables we introduce, whose number is related to the size of the arithmetic case and needs to be estimated. A large number of auxiliary variables will make the difficulty of solving soar. In general, to represent an integer between 0 and \(\varsigma \), \(\left[ {{\log }_{2}} \varsigma \right] +1\) discretized auxiliary variables need to be introduced, where \([\varsigma ]\) denotes the largest integer that does not exceed \(\varsigma \). Of course, if there are non-integer values introduced in the calculation example, then it is necessary to introduce an approximate representation. First, we introduce the precision matrix as follows:
$$\begin{aligned} p=\left[ {{\left( \frac{1}{2} \right) }^{0}},{{\left( \frac{1}{2} \right) }^{1}},{{\left( \frac{1}{2} \right) }^{2}},\ldots \right] . \end{aligned}$$
(28)
Then the real numbers \({{\varpi }_{i}}\) \((i=1,\ldots ,L)\) in some interval can be approximated as follows.
$$\begin{aligned} {{\varpi }_{i}}\approx {{p}^\texttt{T}}{{b}_{i}}\text {=}\left[ {{\left( \frac{1}{2} \right) }^{0}},{{\left( \frac{1}{2} \right) }^{1}},{{\left( \frac{1}{2} \right) }^{2}},\ldots \right] ^\texttt{T}{{b}_{i}} \end{aligned}$$
(29)
where \({{b}_{i}}\in {{\{0,1\}}^{L}}\) \((i=1,\ldots ,L)\). If the error is expressed in terms of \(\phi \), the error satisfies the following relation:
$$\begin{aligned} \phi \le {{\left( \frac{1}{2}\right) }^{L}}. \end{aligned}$$
(30)
In this way, we can rewrite (24) and (25) as follows.
$$T={{\delta}_{1}}+2{{\delta}_{2}}+\ldots+{{2}^{m}}{{\delta }_{m}}+{{\left(\frac{1}{2}\right)}^{0}}{{\sigma }_{1}}+{{\left(\frac{1}{2}\right)}^{1}}{{\sigma}_{2}}+\ldots+{{\left(\frac{1}{2}\right)}^{L-1}}{{\sigma }_{L}}$$
(31)
$${{T}_{k}}={{\delta}_{1k}}+2{{\delta}_{2k}}+\ldots+{{2}^{{{m}^{‘}}}}{{\delta }_{{{m}^{‘}}k}}+{{\left(\frac{1}{2}\right)}^{0}}{{\sigma }_{1k}}+{{\left(\frac{1}{2}\right)}^{1}}{{\sigma}_{2k}}+\ldots+{{\left(\frac{1}{2}\right)}^{{{L}^{‘}}-1}}{{\sigma }_{{{L}^{‘}}k}}$$
(32)
The positive real numbers can be approximated using integer auxiliary variables. \({{\sigma }_{j}}\) \((j=1,2\ldots ,L)\) and \({{\sigma }_{jk}}\) \((j=1,2,\ldots ,{{L}^{‘}},k\in V)\) are used to approximate the decimal part. The number of binary variables used is related to the required approximate accuracy, as shown in Formula (28).
Thus, the model under this objective can be represented as follows, Eqs. (18)–(22), (24)–(25), (31)–(32).
$$\text{(P4)}\qquad{{H}_{2}}={{\varepsilon}_{1}}{{H}_{Y}}+{{\varepsilon}_{2}}{{H}_{B}}+{{\varepsilon}_{3}}{{H}_{C}}+{{\varepsilon}_{4}}{{H}_{D}}+{{\varepsilon}_{5}}{{H}_{E}}+{{\varepsilon}_{6}}{{H}_{F}}+{{\varepsilon}_{7}}{{H}_{Z}}$$
(33)
In (33), \({{\varepsilon }_{i}}\) \((i=1\ldots ,7)\) are weights for each objectives. The model does not satisfy the QUBO form, because \({{H}_{Z}}\) is a quadrinomial binary polynomial, which needs to be degenerated. Next, we provide some analysis of the \({{H}_{Z}}\). First, to make it easier to show our results, we perform a variable substitution, as follows:
$$\begin{aligned} \eta \text { =}\sum \limits _{(r,{{r}^{‘}})\in A}{\sum \limits _{t=1}^{N-1}{{{c}_{r{{r}^{‘}}}}}}{{x}_{r,t,k}}{{x}_{r,t+1,k}}. \end{aligned}$$
(34)
The total number of tasks is N, and \(\eta \) contains \(({{N}^{2}}-3N+3)(N-1)\) monomials. Then \({{H}_{Z}}\) can be expanded as follows.
$$\begin{aligned} {{H}_{Z}}=\sum \limits _{k\in V}{({{\eta }^{2}}-2\eta T+2\eta {{T}_{k}}+{{T}^{2}}+T_{k}^{2}-2T{{T}_{k}})} \end{aligned}$$
(35)
In the \({{H}_{Z}}\), \({{\eta }^{2}}\) is a quadrinomial binary polynomial, \(-2\eta T\) and \(2\eta {{T}_{k}}\) are cubic binary polynomials, and \({{T}^{2}}\), \(T_{k}^{2}\) and \(-2T{{T}_{k}}\) are all quadratic binary polynomials, so we need to reduce \({{\eta }^{2}}\), \(-2\eta T\) and \(2\eta {{T}_{k}}\). The number of quardrinomial binary monomials in \({{\eta }^{2}}\) is represented by \({{\tau }_{4}}\), and \({{\tau }_{4}}\) is as follows:
$$\begin{aligned} {{\tau }_{4}}={{(({{N}^{2}}-3N+3)(N-1))}^{2}}|V|. \end{aligned}$$
(36)
Note that
$$\begin{aligned} {{x}^{n}}=x (n\in {{\mathbb {Z}}^{+}}),x\in (0,1) \end{aligned}$$
(37)
where \({{\mathbb {Z}}^{+}}\) represents the set of all positive integers. Equation (37) indicates that any power of the binary variable itself is equal to itself, and thus, \(\tau _{4}^{‘}\) quardrinomial monomial can be directly reduced, and its specific number is as follows.
$$\begin{aligned} \tau _{4}^{‘}=(({{N}^{2}}-3N+3)(N-1))|V| \end{aligned}$$
(38)
Therefore, the number of quadrinomial polynomials that truly need to be reduced is \({{\tau }_{4}}-\tau _{4}^{‘}\) terms. Looking at the part of cubic polynomial, the number of cubic monomials in \({{H}_{Z}}\) is represented by \({{\tau }_{3}}\), and then \({{\tau }_{3}}\) is as follows:
$$\begin{aligned} {{\tau }_{3}}=(m+L+{{m}^{‘}}+{{L}^{‘}})({{N}^{2}}-3N+3)(N-1)|V|. \end{aligned}$$
(39)
Then, the number of all polynomials in \({{H}_{Z}}\) that need to be descended \(\tau \) is as follows:
$$\begin{aligned} \tau ={{\tau }_{3}}+{{\tau }_{4}}-\tau _{4}^{‘}. \end{aligned}$$
(40)
At least \(\tau \) binary auxiliary variables must be introduced to complete the descending order according to a paper35. Due to the number of auxiliary variables introduced, the processing is more complex and it is difficult to calculate using existing quantum computers. So this model will not be introduced so far in this paper.
Arc model
In this section we will describe the arc model. The core idea of arc model is that the sequence of tasks before and after execution is regarded as an arc connected between nodes, and building the model with arc as the basic unit can reduce the dimension. The arc model also has a QUBO form with the same parameter settings as the node model, and the decision variables are shown below.
\({{\upsilon }_{a,t,k}}\) binary variable, equal to 1 if arc a is assigned to AGV k in sequence t, 0 otherwise.
As with the node model, we first explore the model with the optimization objective of minimizing the total travel time.
$$\text{(P5)}\qquad{{H}_{3}}={{\beta }_{1}}{{H}_{G}}+{{\beta }_{2}}{{H}_{J}}+{{\beta }_{3}}{{H}_{L}}+{{\beta }_{4}}{{H}_{M}}+{{\beta }_{5}}{{H}_{O}}+{{\beta }_{6}}{{H}_{Q}}+{{\beta }_{7}}{{H}_{S}}+{{\beta }_{8}}{{H}_{U}}$$
(41)
$$\begin{aligned} {{H}_{G}}&=\sum \limits _{k\in V}{\sum \limits _{a\in A}{\sum \limits _{t=1}^{N-1}{{{c}_{a}}}}}{{\upsilon }_{a,t,k}} \end{aligned}$$
(42)
$$\begin{aligned} {{H}_{J}}&={{\sum \limits _{k\in V}{\left( 1-\sum \limits _{a\in \theta _{0}^{+}}{{{\upsilon }_{a,1,k}}}\right) }}^{2}} \end{aligned}$$
(43)
$$\begin{aligned} {{H}_{L}}&=\sum \limits _{k\in V}{\sum \limits _{{\begin{matrix} a\ne {{a}_{1}} \\ a\in \theta _{n}^{-} \\ {{a}_{1}}\in A \end{matrix}}}{\sum \limits _{t=1}^{N-2}{{{\upsilon }_{a,t,k}}{{\upsilon }_{{{a}_{1}},t+1,k}}}}} \end{aligned}$$
(44)
$$\begin{aligned} {{H}_{M}}&=\sum \limits _{k\in V}{\sum \limits _{{\begin{matrix} a\ne {{a}_{1}} \\ a\in A \\ {{a}_{1}}\in A \end{matrix}}}{\sum \limits _{t=1}^{N-1}{{{\upsilon }_{a,t,k}}}}}{{\upsilon }_{{{a}_{1}},t,k}} \end{aligned}$$
(45)
$$\begin{aligned} H_O&= \sum _{r\in R}\left( 1-\sum _{k\in V}\sum _{a\in \theta _r^-}\sum _{t=1}^{N-2}v_{a,t,k}\right) ^2 \end{aligned}$$
(46)
$$\begin{aligned} H_Q&= \sum _{k\in V}\left( 1-\sum _{a\in \theta _0^+}\sum _{t=1}^{N-2}v_{a,t,k}\right) ^2 \end{aligned}$$
(47)
$$\begin{aligned} H_S&= \sum _{k\in V}\left( 1-\sum _{a\in \theta _n^-}\sum _{t=2}^{N-1}v_{a,t,k}\right) ^2 \end{aligned}$$
(48)
$$\begin{aligned} {{H}_{U}}&=\sum \limits _{k\in V}{\sum \limits _{r\in R}{\sum \limits _{t=1}^{N-2}{{{\left( \sum \limits _{a\in \theta _{r}^{-}}{{{\upsilon }_{a,t,k}}}-\sum \limits _{{{a}_{1}}\in \theta _{r}^{+}}{{{\upsilon }_{{{a}_{1}},t+1,k}}}\right) }^{2}}}}}. \end{aligned}$$
(49)
\({{\beta }_{i}}\) \((i=1,\ldots ,8)\) are weights for the corresponding objective. The objective function (42) is to minimize the total travel time of the AGV. We want all AGVs to be executed in the first order a task arc that starts with a virtual start task, so we add the minimization function (43). The minimization function (44) means that the last task completed by each AGV must be a virtual end task. We want to complete at most one task arc in a certain order of an AGV, so we add the minimization function (45). The minimization function (46) indicates that for each actual task, we want a certain task arc with it as the starting node to be assigned to an AGV in a certain order of completion, and we want the virtual start task to be completed only once for each AGV, so we add the minimization function (47). Similarly, for each AGV, its virtual end task can only be completed once, so we add the minimization function (48). The minimization function (49) ensures that for each AGV, it is must to satisfy the flow balance when performing the task arc.
Next, we show a model with the goal of minimizing the makespan as follows, Eqs. (42)–(49).
$$\begin{aligned} \text {(P6)}\qquad {{H}_{4}}&={{\lambda }_{1}}{{H}_{V}}+{{\lambda }_{2}}{{H}_{J}}+{{\lambda }_{3}}{{H}_{L}}+{{\lambda }_{4}}{{H}_{M}}+\nonumber \\&{{\lambda }_{5}}{{H}_{O}}+{{\lambda }_{6}}{{H}_{Q}}+{{\lambda }_{7}}{{H}_{S}}+{{\lambda }_{8}}{{H}_{U}}+{{\lambda }_{9}}{{H}_{W}} \end{aligned}$$
(50)
$$\begin{aligned} {{H}_{V}}&=T \end{aligned}$$
(51)
$$\begin{aligned} {{H}_{W}}&=\sum \limits _{k\in V}{{{\left( T-\sum \limits _{a\in A}{\sum \limits _{t=1}^{N-1}{{{c}_{a}}{{\upsilon }_{a,t,k}}}}-{{T}_{k}}\right) }^{2}}}. \end{aligned}$$
(52)

Wanda Parisien is a computing expert who navigates the vast landscape of hardware and software. With a focus on computer technology, software development, and industry trends, Wanda delivers informative content, tutorials, and analyses to keep readers updated on the latest in the world of computing.


